Decibel-tutoriaal: dB en dBm vs. Gain and Milliwatts

Die konsep van 'n desibel (dB) is begryplik moeilik en verwarrend vir iemand wat bloot daaraan bekendgestel word. Om spesifikasies vir versterking, drywing en spanning (en stroom, maar nie so gereeld nie) te kombineer wat dB, dBm, dBW, watt, milliwatt, spanning, millivolt, ens. Kombineer, moet u heen en weer omskakel tussen lineêre waardes en desibelwaardes. Hierdie kort tutoriaal help om die verskil tussen werk met desibel en lineêre waardes te verduidelik.

Logaritmes (logs) is eers in die vroeë 1600's uitgedink deur die Skotse wiskundige John Napier, as 'n instrument om vermenigvuldigings- en delingsbewerkings te vereenvoudig deur dit om te skakel na vinniger en minder foutiewe optel- en aftrekoperasies. Dit word moontlik gemaak omdat die vermenigvuldiging van twee getalle uitgedruk as soortgelyke basisgetalle met eksponente bewerkstellig kan word deur bloot die eksponente bymekaar te tel. Die verdeling van dieselfde getalle word bewerkstellig deur die eksponente af te trek. Dit is een van die wette van eksponente en lyk so:

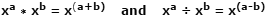
Gebruik werklike getalle as voorbeeld, waar x = 10, a = 4, b = 1:

Die eksponentwet werk vir enige basisnommer, nie net vir 10 nie. Om te weet:

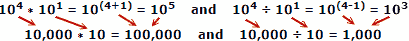
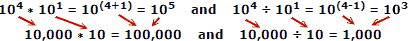
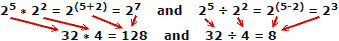
Mense is geneig om minder foute te maak as hulle getalle optel en aftrek, dus is die voordeel van logaritmes duidelik. Onthou dat logaritmes ontwikkel is voordat outomatiese meganiese of elektroniese rekenaars beskikbaar was. 'N Skyfreël benut die eienskappe van logaritmes vir berekening, maar dit is 'n aparte hoofonderwerp.

Dit is eenvoudige voorbeelde, maar geld vir enige basis of eksponent. As u nie 'n sakrekenaar het nie, benodig u 'n tabel met syfers en die ooreenstemmende logaritmes om dit vir algemene toepassingsdoeleindes te gebruik. Vroeë log-tabelle het volumes gevul, afhangende van die afstand tussen getalle (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3, ens.). Die goeie nuus vir skeppers van logaritmietabelle is dat slegs 'n enkele 'dekade' van getalle (bv. 1 tot en met 10) nodig is, aangesien elke dekade wat voorlê of afsluit, 'n eenvoudige veelvoud is van 'n krag van 10.

Opmerking: ek gebruik basis 10 in hierdie bespreking, want dit is die basis van ons gewone getallestelsel - vandaar die term 'gemeenskaplike logaritme' vir basis 10-logs. U het moontlik gehoor van natuurlike logaritmes, wat die basis van e gebruik, maar e word nie baie gereeld gebruik vir die berekening van skaliese elektriese krag, spanning en stroomhoeveelhede nie (hoewel dit gebruik word wanneer fasehoeke ingesluit word, dit wil sê Euler se identiteit). Natuurlike logaritmes word geskryf as ln (x) sonder die 'e' subskrip, terwyl meestal basiese 10 logaritmes geskryf word bloot as log (x) sonder die 10 subskrip; dit wil sê, nie loge (x) of log10 (x) onderskeidelik nie.

Per basis = 10 logtabel:

Semi-logaritmiese 5 Cycles Engineering Grafiekpapier - RF CafeDie uitsondering en spesiale geval is logx (0) = Ongedefinieerd. Dit is so omdat daar geen krag is waaraan u enige getal kan verhoog en 0 (nul) kan kry nie. U kan asimptoties nul nader, maar u kan nie tot nul kom nie. Daar sal nooit die getal nul op 'n logskaal verskyn nie; hulle loop gewoonlik van een of ander krag van 10 na 'n ander krag van tien. 'N Voorbeeld van loggrafiekpapier word regs getoon. Dit het 5 'siklusse' of 'dekades' van reikwydte. Let daarop dat daar geen nul op die y-as is nie.

Die basis-10 (gemeenskaplike) logaritme van 'n getal is dan die eksponent waarna 10 opgevoed moet word om die nommer te kry. Met ander woorde, aangesien 10 verhoog tot die krag van 2 gelyk is aan 100 (102 = 100), is die basis-10-log van 100 2 (log10 100 = 2).

Dit is die basiese wet van logaritmes:


Voer dieselfde vermenigvuldigings en verdelings uit as aan die bokant van die bladsy deur gebruik te maak van werklike logaritmes:



Dit is goed, maar waarmee u eindig, is die logaritme van die nommer wat u soek. Vraag: Behalwe vir 'n eenvoudige voorbeeld soos hierdie, hoe kry u die antwoord wat u nodig het? Antwoord: Soek die antilogaritme (antilog) van die resultaat op. In hierdie geval:

'N Strenger, en waarskynliker voorbeeld met getalle wat nie heelgetalle van 10 is nie, lyk dalk soos volg:




 HP-35 sakrekenaar (wikipedia) - RF CafeVanaf die logaritme van 'x' is gelyk aan 1.8444, die antilog is gelyk aan 'x', wat 69.9 is



Ek het my sakrekenaar gebruik om die logs en hulpprogramme vir daardie getalle op te soek, maar voor 1972 toe Hewlett Packard (HP) hul wetenskaplike sakrekenaar HP-35 voorgestel het, was die gemiddelde persoon sonder toegang tot 'n hoof- of universiteitsrekenaar nodig om 'n log te gebruik tabel om sulke berekeninge uit te voer.

Wie pla die logaritmes van vandag, vra u dalk? Baie mense, ook ek, word gereeld by die berekening van kaskade-stelselparameters soos geraasfiguur (NF) en afsnitpunte (IP) bereken. Eenvoudige optel en aftrek van dBm- en drywingsdBm-waardes werk nie met NF en IP nie. Die beheerformules gebruik vermenigvuldiging en verdeling van lineêre versterking en drywingswaardes, wat eerstens dB en / of dBm moet omgeskakel word na lineêre getalle (versterkingsverhouding en mW) deur gebruik te maak van hulpmiddels, die berekening van die kaskade uit te voer, en dan die resultaat weer om te skakel na dB en / of dBm met behulp van logboeke.

Nie alle stelselkaskade-bedrywighede hoef heen en weer omgeskakel te word nie. Byvoorbeeld, as slegs die totale stelselvermeerdering en / of uittree-drywingsvlak benodig word, kan berekeninge met óf lineêre eenhede (mW en vermenigvuldigers) óf logaritmiese eenhede (onderskeidelik dBm en dB) gedoen word.

Die definisie van 'dB' en 'dBm'

'N Desibel (dB) in elektriese ingenieurswese word gedefinieer as 10 maal die basis-10-logaritme van 'n verhouding tussen twee drywingsvlakke; bv. Pout / Pin (wins, met ander woorde). Om te weet:

Alle winste groter as 1 word dus uitgedruk as positiewe desibel (> 0), en winste van minder as 1 word uitgedruk as negatiewe desibel (<0). Let op dat die gevalle van die meeste van ons ondervind, dat die lineêre verhouding van P1 / P2 'n positiewe getal (> 0) moet wees, aangesien die logaritme van 0 ongedefinieerd is en die logaritme van negatiewe getalle kompleks is (dit bevat 'n werklike en 'n denkbeeldige deel. ). Die dB-waarde kan egter teoreties enige waarde aanneem tussen −∞ en + ∞, insluitend 0, wat 'n wins van 1 [10 * log (1) = 0 dB] is.

'dBm' is 'n desibel-gebaseerde krageenheid waarna verwys word na 1 mW. Aangesien 0 dB van wins gelyk is aan 'n toename van 1, is 1 mW krag 0 dB groter as 1 mW, of 0 dBm. Net so is 'n drywingseenheid van dBW desibel relatief tot 1 W krag.


Gevolglik is alle dBm-waardes groter as 0 groter as 1 mW, en alle dBm-waardes kleiner as 0 is kleiner as 1 mW (sien Fig. 1). Byvoorbeeld, + 3.01 dBm is 3.01 dB groter as 1 mW; dit wil sê, of 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm is 3.01 dB minder as 1 mW; dit wil sê, of 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Die volgende tabel gee enkele numeriese voorbeelde, sodat u die verband tussen mW en dBm kan sien. Dieselfde stel waardes op 'n logaritmiese skaal sou 'n reguit lyn lewer. As gevolg van die logaritmiese verhouding, bundel die grafiek die kleiner waardes teen die linker vertikale as. Vir die duidelikheid word 'n vergrote weergawe van die 0 tot 1 mW-streek ingestel.

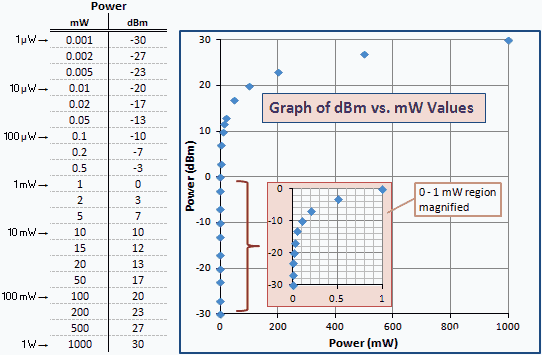
Figuur 1 - Grafiek van drywing in eenhede van dBm vs. mW

Figuur 2 is 'n tabel en grafiek van dB teenoor lineêre versterkingsverhoudings soortgelyk aan die dBm teenoor mW in Figuur 1. Let daarop dat die getalle en kurwes presies dieselfde is; slegs die asetikette word verander. Dit is omdat dBm 'n krageenheid is wat uitgedruk word in dB relatief tot 1 mW (0 dBm).

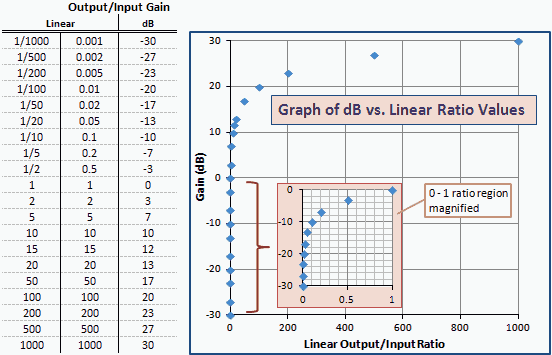
Figuur 2 - Grafiek van wins in eenhede van dBm teenoor lineêre verhouding

Fundamenteel is wins 'n vermenigvuldigingsfaktor. As voorbeeld kan 'n versterker 'n versterking hê wat die sein verhoog met 'n faktor van 4 (dit wil sê 4x) van inset na uitset (sien fig. 3). As 'n 1 mW (0 dBm) sein in die versterker gevoer word, dan kom 1 mW * 4 = 4 mW uit. Wat die desibel is, is 'n faktor van 4 gelyk aan 10 * log (4) = 6.02 dB, dus 0 dBm in plus 6.02 dB winsopbrengste + 6.02 dBm by die uitset.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

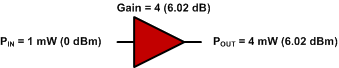
Figuur 3 - Enkel versterkerwins.

Kombinasies van winste (lineêr en dB) met positiewe waarde

As 'n versterker met 'n toename van 4 in serie is met 'n tweede versterker met 'n toename van 6, dan is die totale wins 4 * 6 = 24. In terme van desibel is 'n faktor van 6 gelyk aan 10 * log (6) = 7.78 dB, en 'n faktor van 24 is gelyk aan 10 * log (24) = 13.8 dB.

Net soos 4 x 6 = 24 (lineêre wins), 6.02 dB + 7.78 dB = 13.8 dB (desibelwins).

As 'n 1 mW sein (0 dBm) in die versterker gevoer word, dan kom 4 mW uit die eerste versterker, en 24 mW kom uit die tweede versterker. Kyk Fig. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Figuur 4 - Gevorderde dubbele versterkerwins.

Kombinasie van wins en verlies (lineêr en dB)
Hierdie volgende voorbeeld wys wat gebeur as 'n versterking <1 ('n verlies) voorkom, waar 'n demper met 'n versterking van 1/6 na die eerste versterker geplaas word in plaas van 'n tweede versterker. Sien Fig. 5.
4 * 1 / 6 = 2 / 3 (lineêre wins). Net so is 6.02 dB - 7.78 dB = −1.76 dB (desibelwins).
Soos met die vorige voorbeeld, as 'n 1 mW sein (0 dBm) in die versterker gevoer word met 'n toename van 4, dan kom 4 mW uit. Daardie 4 mW gaan dan in die verswakker met 'n lineêre toename van 1 / 6 en kom uit op 'n drywingsvlak van 4 / 6 mW (2 / 3 mW).
Die totale wins in hierdie geval is 4 / 6 = 2 / 3, dus sal die uitsetkrag eintlik minder wees as die insetkrag.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Figuur 5 - Gevorderde versterkerversterker en verswakker.

12 mW + 34 mW + 8 mW + 20 dB

Aanvullende inligting oor logaritmes
Logaritmes van produkte
Die eienskap van logaritmes wat hierbo impliseer, sê die volgende, en is die basis om logaritme-waardes by te voeg en af ​​te trek in plaas daarvan om hul lineêre ekwivalente te vermenigvuldig.

'h * j / k * m / n' kan 'n kaskade van komponente voorstel met drie toestelle (h, j en m) elk met versterking> 1 en twee toestelle (k en n) elk met 'n versterking <1 (sien Fig. 6). Die totale stelselwins kan bereken word deur al die lineêre versterkingswaardes saam te vermenigvuldig of al die desibel versterkingswaardes bymekaar te tel.

Figuur 6 - Gekaskadeerde komponente

Logaritmes van eksponente
Die volgende is belangrik om te verstaan ​​waarom kragverbetering in terme van krag 10 * log (Pout / Pin) dB is, terwyl kragverbetering in terme van spanning 20 * log (Vout / Vin) dB is.


wat so is omdat cf gelyk is aan c vermenigvuldig met homself 'f' keer. Byvoorbeeld, as f = 4:


Kragstoot gebaseer op krag teen kragsterkte gebaseer op spanning
Kragwins is Pout / Pin, en spanning versterking is Vout / Vin. Kragverbetering gebaseer op 'n drywingsverhouding in desibel word gedefinieer as 10 * log (Pout / Pin). Kragverbetering in terme van spanning is [(Vout2 / R) / (Vin2 / R)], aangesien dit volgens Ohm se wet P = V2 / R is. Die 'R' in die noemers kanselleer die verlaat van Vout2 / Vin2, wat gelyk is aan (Vout / Vin) 2, soos omskryf deur die reël van eksponente wat sê ac / bc = (a / b) c. vandaar:

Belangrike Nota: Spanningstoename in terme van spanning is 10 * log (Vout / Vin) dB, dieselfde as met drywingswins in terme van drywing. Die 20 * log (Vout / Vin) dB-vergelyking is slegs van toepassing wanneer spanning verkry word in terme van spanning. Dit is 'n algemene punt van verwarring.


Geen bewerking in wiskunde is arbitrêr nie, en dit is die rede waarom 'n seinverliesverlies (versterking <1) as 'n negatiewe waarde uitgebeeld word, en dus tydens 'n kaskadeberekening afgetrek word. Dit is 'n eenvoudige demonstrasie, maar noemenswaardig.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

As u 'n radiostasie wil bou, versterk u FM-radiosender of benodig enige ander FM toerusting, kontak ons ​​gerus: [e-pos beskerm].

Los 'n boodskap 

boodskap Lys